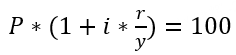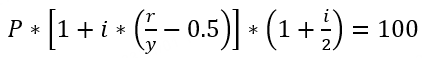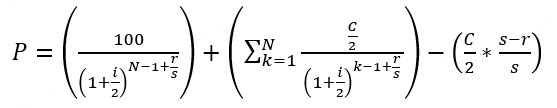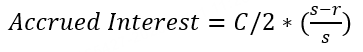Terms | Explainations |
Bond Price | The bond price is the price at which you purchase the bond, and may fluctuate at any time during trading hours. |
Yield to Maturity,YTM | It refers to the annualized rate of return that an investor will receive if they hold the bond until its maturity date, assuming that both the principal and interest of the bond are paid on time (excluding the cost of transaction commissions). The present value obtained by discounting all future cash flows of the bond at the yield to maturity should equal the purchase price. That is, the total present value of future interest payments and final principal repayment should equal the bond's current market price. The calculation formula for YTM varies for different types of bonds:
Related Parameters in the Formula:
|
Coupon Payment Frequency | The coupon payment frequency refers to the regular time intervals at which interest payments are made on a government bond, such as twice a year or once a year. U.S. Treasury notes and bonds typically have a fixed schedule of making interest payments twice a year. |
Remaining Term | The number of years left from the current purchase date until the maturity of the bond. |
Maturity Date | The expiration date of the bond. |
Execution date | The date when the transaction is agreed upon, but the transfer of bond ownership has not yet occurred. |
Settlement date | he final completion date of the transaction, where the buyer must pay the seller, and the seller transfers the assets to the buyer. This is usually the day after the execution date. Accrued interest is calculated based on the settlement date. |
Bid Price | The reference price for buying bonds from the platform. The quoted price for T-Bills is usually the interest rate, i.e., the Discount Rate; for Bonds and Notes, it is typically the price. Quotations do not include transaction commissions and accrued interest. |
Ask Price | The reference price for selling bonds that one owns. It represents the price buyers are willing to pay. |
Mid-Price | The midpoint between buying and selling prices on the market. It can be used as a reference for investors as it often reflects the supply and demand situation in the market. |
Duration | A measure of the sensitivity of a bond's price to changes in interest rates, which can help predict the direction and magnitude of bond price changes when market interest rates rise or fall. |
Modified Duration | A variant of duration, typically used to measure the absolute change in a bond's price due to interest rate changes. |
Convexity | A financial metric measuring the non-linear response of a bond's price to changes in interest rates. Convexity is the second derivative of the bond's price with its expected yield, considering the curvature of the bond price when market interest rates change. |
Accrued Interest | Accrued interest is not a fee but the interest paid by the buyer to the seller for the holding period. Although bonds generally pay interest semi-annually, accrued interest is calculated daily after purchase, and the buyer must pay this amount to the seller during a transaction. Accrued interest is reset and recalculated after each interest payment. Where C = coupon payment, s = total days in the current coupon period, r = remaining days in the current coupon period. Example to illustrate accrued interest: Suppose there is a Treasury bond with a face value of $1,000 and a coupon rate of 5%, accruing interest twice a year, with interest dates on June 30 and December 31. If you purchase this bond on September 1, and the next interest payment date is December 31, you need to pay the seller the accrued interest at the time of purchase. The calculation of accrued interest is as follows: Face Value × Coupon Rate × (Number of Unpaid Days / 365) With unpaid days from June 30th to September 1st. totaling 63 days, and the bond face value at $1,000 with a 5% coupon rate, the accrued interest is: Accrued Interest = $1,000 × 5% × (63 days / 365 days) ≈ $8.63 Therefore, if you purchase this bond on September 1, you need to pay the seller about $20.68 in accrued interest to compensate for the interest they would have earned. Then, on December 31 of that year, you will receive the full interest payment. (Note: The above example uses a general formula for calculating accrued interest for ease of understanding. Each institution may have different definitions of the "interest coefficient," and actual calculations should be based on specific results.) |